이번 시간에는 코로나에 걸렸을지 가능성을 수학적으로 도출해보는 과정을 알아본다. 진단키트가 100% 확률이 아니므로, 위양성 위음성을 고려한 감염 가능성을 판단해야 한다. 이걸 해보면 전국민을 몽땅 검사하지 않는 이유를 이해할 수 있다.
들어가기에 앞서, 조건부 확률에 대한 지난글을 보고오면 보다 수월하다.
전체 확률의 법칙
베이즈 정리 유도에 앞서 조건부 확률의 수식을 이용해서 전체 확률의 법칙 (law law of total probability) 또는 전확률 정리라 부르는 형태로 나타낼 수 있다. 베이즈 정리로 가기위한 거쳐가는 단계라고 보면 된다.
사건 A는 표본공간 S의 부분집합이고, 표본공간 S는 사건 B1, B2, B3, … , Bk 개로 나눌 수 있을 때 전확률 공식이 성립한다.
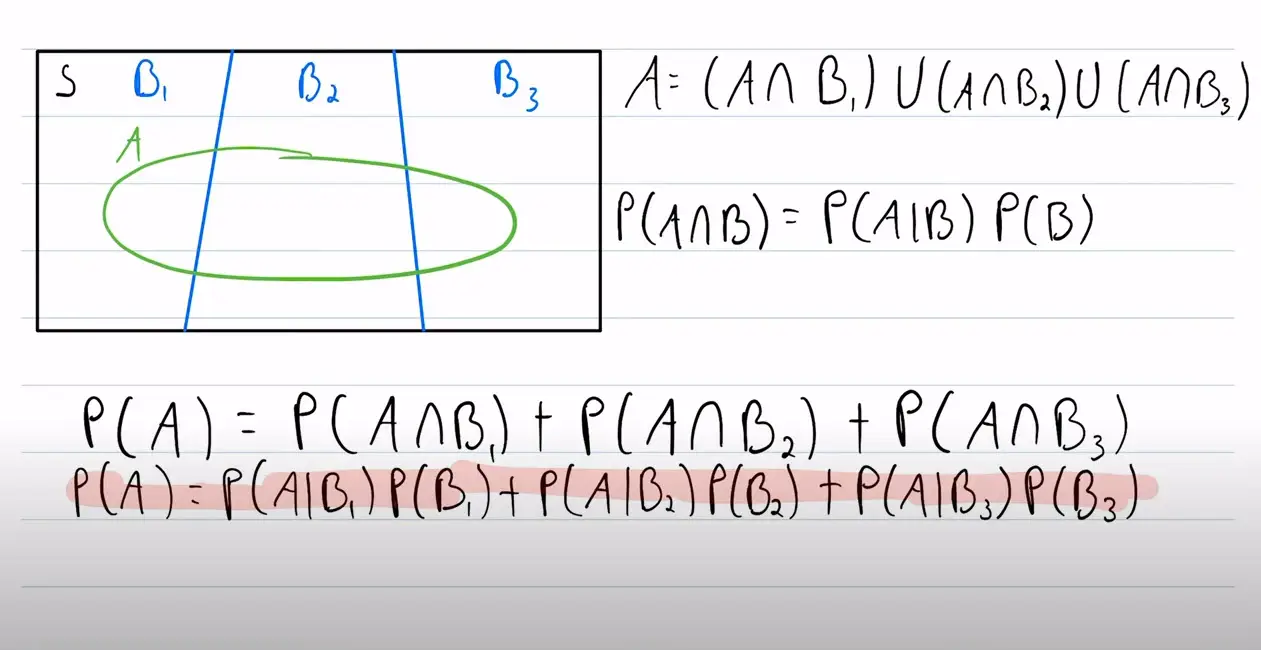
표본공간 S가 B1, B2, B3로 나눌 수 있고, S의 부분집합인 사건 A가 있는 벤 다이어그램을 가정한다. 여기서 A는 B1 B2 B3와 각각 겹치는 교집합 영역이 생긴다. 그렇다면 A는 교집합 영역 3개의 합으로 나타낼 수 있다.
P(A) = P(A∩B1) + P(A∩B2) + P(A∩B3)
두 사건이 독립이 아닐 때, 교집합의 확률은 조건부 확률 공식 P(A|B) = P(A∩B) / P(B) 을 변환하여 P(A∩B) = P(A|B) P(B) 와 같이 나타낼 수 있다. A와 B의 교집합 사건 확률은 B확률 곱하기 B가 일어났을 때 A가 일어날 확률이다. 벤다이어그램을 보면서 생각하면 이해하기 쉽다.
조건부 확률 공식을 이용하여 위 식을 다시 써보자.
P(A) = P(A|B1) P(B1) + P(A|B2) P(B2) + P(A|B3) P(B3)
이것이 전체 확률의 법칙이다. 표본공간 S의 부분집합인 사건 A의 확률을, 표본공간을 구성하는 B1~Bk 와의 교집합의 합으로 나타낸 것이다. 그리고 그 교집합은 조건부 확률 공식을 이용하여 나타낼 수 있다.
예제문제
전체 확률의 법칙을 이용하여 예제 문제를 풀어보자.
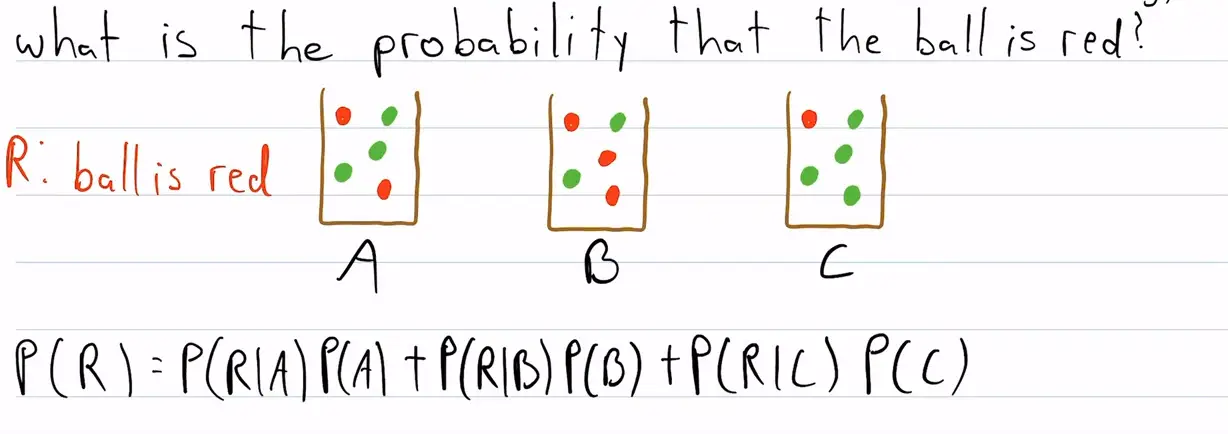
A통에는 빨간공 2개 녹색공 3개 / B통에는 빨간공 3개 녹색공 2개 / C통에는 빨간공 1개 녹색공 4개가 들어있다. 어느 통에서 뽑을지는 동일한 확률로 랜덤하게 결정된다고 할 때, 공을 하나 뽑아서 빨간공이 나올 확률을 구하라.
이 문제는 사실 2초면 답할 수 있다. 빨간공 6개인데 전체 15개니까 6/15잖아? 라고 말이다. 문제가 단순하게 주어졌으니 가능한 것이고 만약 A B C 에서 뽑을 확률을 다르게 준다면 어떻게 할 것인가. 전체 확률의 법칙을 이용해서 풀어야 한다.
공을 뽑는다는 행위가 표본공간 S가 되고, 그 중에 빨간공을 뽑는 사건이 R이다. 공은 A, B, C 셋 중에 하나에서 뽑게 되므로 표본공간 S=A+B+C 이다.
위에 소개한 벤다이어그램과 같은 상황이며, R의 확률은 A, B, C와의 교집합들의 합으로 나타낼 수 있다.
P(R) = P(A∩R) + P(B∩R) + P(C∩R)
여기서 각 교집합을 조건부 확률 공식을 이용하여 치환한다.
A에서 뽑고 빨간공이 나왔을 확률 = A에서 뽑았는데 빨간공일 확률 X A에서 뽑을 확률
P(R) = P(R|A) P(A) + P(R|B) P(B) + P(R|C) P(C)
문제에서 P(A) = P(B) = P(C)= 1/3 이고 각 통에서 뽑았는데 빨간공일 조건부 확률은 아래와 같다.
P(R|A) = 2/5
P(R|B) = 3/5
P(R|C) = 1/5
P(R) = (2/5)*(1/3) + (3/5)*(1/3) + (1/5)*(1/3) = 6/15
이렇게 풀기전에 직관적으로 계산한 값과 동일한 답을 얻을 수 있다.
전체확률의 법칙 설명 및 예시문제 출처
베이즈 정리 (Bayes’s formula)
조건부 확률을 계산하는 또다른 중요한 방법은 베이즈 정리이다. 지금까지의 조건부 확률은 많은 정보가 주어져 있어서 표본공간의 각 영역의 확률을 모두 구하는 것이 용이했다.
그러나 베이즈 정리는 현실 세계에서 우리가 가질 수 있는 제한적인 정보로 확률적 추론을 할 수 있게 해주는 방법이다. 감을 잡기 위해 베이즈 정리를 어디에 쓰는지부터 살펴보자.
베이즈 정리를 설명하는 많은 문서들에서 꼭 등장하는게 바로 검사시약 문제이다. 코로나 검사를 하는 경우로 문제를 만들어보자.
코로나 걸린 환자에게 진단키트로 검사를 했는데 양성판정할 확률이 95%라고 하자. 즉 이 진단키트는 코로나 걸린 사람중에 95%를 확진판정해서 걸러낼 수 있는 신뢰도가 있다.
그런데 현실에서는 이 사람이 코로나에 걸렸는지 모른채로 검사를 한다. 한명을 검사해봤는데 양성이 나왔다. 그러면 이 사람은 코로나일가 아닐까? 코로나일 확률이 95%일까? 코로나가 확실할 경우에 이 사람을 양성판정할 확률이 95%라는 말이지 코로나에 걸렸을 확률은 모른다.
이러한 경우에 바로 베이즈 정리를 사용하는 것이다. 코로나 걸렸을 때 양성판정될 확률 P(B|A)를 알고 있을 때, 그럼 양성판정 됐을 때 코로나일 확률 P(A|B)는 얼마인지를 역으로 구하는 방법이다.
베이즈 정리 공식은 마찬가지로 조건부 확률을 이용해 다음과 같이 유도한다.
P(A∩B) = P(A|B)P(B) = P(B|A)P(A)
여기서 양 변을 P(B) 로 나눠주면 베이즈 정리가 된다.
P(A|B) = P(B|A)P(A) / P(B)
B의 확률은 A와의 교집합과 A가 아닌 부분과의 교집합의 합으로 나타낼 수 있다. 앞서 설명했던 전체확률의 법칙이며 이를 이용해 P(B) = P(B|A)P(A) + P(B|Aᶜ)P(Aᶜ) 와 같이 나타낼 수 있다.
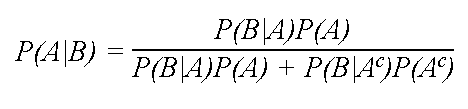
베이즈 공식에서 각각의 확률은 다음과 같은 의미를 갖는다.
P(A|B) : 사후확률 (posterior probability) 사건 B 발생후에 A의 확률
P(A) : 사전확률 (prior probability) 사건 B 발생전에 A의 확률
P(B|A) : 가능도 또는 우도 (likelihood) 사건 A가 발생한 경우 사건 B의 확률
P(B) : 정규화 상수 (normalization constant)
이걸 다 파헤쳐서 이해하려고 하면 헷갈린다. 사건 A의 확률 P(A)을 알고 있었는데 사건 B가 발생하였고 그러면 A의 확률은 어떻게 변하는지를 나타낸다고 보면 된다. 새로운 정보가 생겨났을 때 기존 확률이 업데이트 되는 개념이다. 다양한 예제문제를 통해 감을 익혀보자.
예제문제1
3개 도시에서 선거가 진행되었다. A 도시에서는 50% 유권자가 민주당을 지지하고 B 도시에서는 60%가 지지하며 C 도시에서는 35%의 유권자가 민주당을 지지한다. 세 도시의 인구 총합 중 40%는 A 도시에, 25%는 B도시에, 35%는 C도시에 거주중이다. 유권자가 민주당을 지지한다면 이 사람이 B에 거주할 확률은 얼마인가
P (B 거주 | 민주당 지지) 를 베이즈 정리로 풀어보면
P(A|B) = P(B|A)P(A) / P(B) = P(B|A)P(A) / [P(B|A)P(A) + P(B|Aᶜ)P(Aᶜ)]
P (민주당 지지 | B 거주) P (B 거주) /
[P (민주당 지지 | A 거주) P (A 거주) + P (민주당 지지 | B 거주) P (B 거주) + P (민주당 지지 | C 거주) P (C 거주)]
= (0.60) * (0.25) / ((0.50) * (0.40) + (0.60) * (0.25) + (0.35) * (0.35))
= (0.15) / (0.20 + 0.15 + 0.1225) = 0.15 / 0.4725 = 0.3175
베이즈 정리의 분모에서 P(B)를 A와 B의 교집합 영역과 A여사건과 B의 교집합 영역으로 나눠서 합하는 형태로 표현했는데, 이 문제에서는 B거주와 B거주가 아닌 부분으로 나눠서 치환하면 된다. B거주가 아닌 부분이 A거주 C거주 두가지이므로 분모에 세 가지 요소의 합으로 된 것이다. (표본공간 S = A거주 + B거주 + C거주 이므로)
예시문제 출처 예일대 페이지
예제문제2
앞서 예를 들었던 코로나 검사문제를 계산해보자. 코로나에 걸린 경우를 사건 A라고 한다. 코로나에 걸리지 않은 경우는 Aᶜ 이다. 진단키트로 테스트를 했을 때 양성이 나온 경우는 B , 음성이 나오는 경우는 Bᶜ 이다.
현실에서 알고 있는 확률은 코로나가 확실한 사람에게 진단키트로 검사했을 때 양성반응이 나오는 확률 P(B|A) 이다. 알고자 하는 것은 양성반응이 나왔을 때 진짜로 코로나일 확률 P(A|B) , 즉 얼마나 검사결과를 믿을 수 있는지의 관점에 대한 문제이다.
문제 : P(B|A)가 0.9 일때 P(A|B) 는 얼마인가
추가로 입수된 정보는 다음과 같다.
1) 코로나에 걸릴 확률은 전체 인구의 1%이다. P(A) = 0.01
2) 위양성, 즉 코로나에 걸리지 않았는데 진단키드로 양성판정을 받는 오류가 5%이다. P(B|Aᶜ) = 0.05
이제 베이즈 정리에 알게된 확률정보들을 대입해보자.
P(A|B) = P(B|A)P(A) / [P(B|A)P(A) + P(B|Aᶜ)P(Aᶜ)]
= (0.9 * 0.01) / [ (0.9 * 0.01) + (0.05 * 0.99) ] = 15.38%
즉 진단키트로 양성이 나왔는데 진짜로 코로나에 걸려있을 확률은 15.38%이다. 생각보다 매우 낮지 않은가? 여기에 주어진 확률 정보들을 가변하면서 정답이 어떻게 변하는지 살펴보자. 재미로…

주어진 확률 요소들을 변화시켰을 때 코로나일 확률이 어떻게 변하는지 보았다. 보면 코로나 아닌데 양성진단할 확률이 낮아질수록, 양성판정일 때 진짜 코로나일 확률은 급격히 높아진다. 즉 검사의 신뢰도가 올라간다는 소리.
이래서 위양성 (거짓양성) 확률을 낮추는게, 통계에서 1종 오류를 줄이는게 중요하다고 하는 것이구나.
예시문제 출처 데이터 사이언스 스쿨
이렇게 조건부 확률에서 전체 확률의 법칙, 베이즈 정리까지 확장하며 살펴보았다. 잠시 쉬어도 갈 겸, 확률통계 공부의 재미도 더할 겸 다음번에는 유명한 몬티 홀 문제를 한번 풀어보겠다.
