유명한 확률 문제인 몬티홀 딜레마 풀이방법에 대해 총정리 해보았습니다. 논란이 있지만 사실 정답은 확실하게 정해진 문제입니다.
직관적인 방식으로 이해하기, 베이즈 정리 수학적으로 증명해보기, 경우의 수 따져보기 여러가지로 생각해봅시다.
몬티홀 문제란?
당신은 몬티홀의 퀴즈쇼에 참가했습니다. 문제를 다맞추고 최종 우승자가 되어 마침내 상품을 받게 되었는데요. 단, 마지막 상품 증정도 하나의 게임을 통해 주어진다고 하네요.
쇼의 진행자 몬티홀 씨는 당신에게 세 개의 닫힌 문을 보여줍니다. 그리고 말합니다. 한 개의 문 뒤에는 자동차가 있고 두개의 문 뒤에는 염소가 있습니다. 하나를 고르라고 하자 당신은 한개의 문을 선택했습니다.
그리고 그 문을 열어 상품을 확인하기 바로 직전!!

몬티홀이 잠시 뜸을 들이더니 당신이 고르지 않은 두 개의 문 중 하나를 열어 보입니다. 그 안에는 염소가 들어 있군요. 몬티홀은 사전에 어느 문 뒤에 무엇이 있는지 알고 있었어요.
쇼의 재미를 위해서 당신이 고르지 않은 문 중에서 염소를 보여준 것이죠. 그리고는 묻습니다.
선택을 바꿀 기회를 드리겠습니다.
바꾸시겠습니까?
과연 여러분이라면 어떻게 하실 건가요? 처음 고른 문의 선택을 유지하실 건가요? 아니면 몬티홀이 열어서 보여준 문 외에 아직 닫혀있는 다른 문으로 선택을 바꿀 것인가요?
이것이 바로 그 유명한 몬티홀 딜레마 입니다. 문제의 조건만 요약하면 다음과 같습니다.
- 문 세개 중 하나의 뒤에는 자동차, 두 개의 뒤엔 염소가 있다.
- 몬티홀은 문 뒤에 무엇이 있는지 사전에 알고있다.
- 당신이 하나를 고르면, 몬티홀이 남은 문 중에서 염소를 열어 보여준다.
당신이 자동차를 골랐다면 염소 두 개 중 임의의 하나를, 당신이 염소를 골랐다면 다른 염소 문을 보여주게 된다. - 문 하나를 열어 염소, 즉 꽝을 보여주고, 닫힌문은 두개가 된 상태에서 당신은 선택을 유지하거나 바꿀 수 있다.
이 몬티홀 딜레마에 대해 직관적으로 또는 수학적으로도 잘 이해할 수 있게 풀이된 설명들을 찾아보았습니다. 그 중에서 가장 베스트들만 추려서 정리한 내용입니다. 한국어로 작성된 몬티홀 해설 중 가장 자세하고 친절하다고 자부합니다. 이걸 보고도 이해가 안되신다면 더이상 한국어로 이해가능한 해설자료는 못찾으실 거에요.
본격적인 정답풀이로 들어가기에 앞서 영상으로 다시 한 번 보는것도 재밌습니다. 카드카운팅으로 카지노 터는 영화 ’21’에 이 몬티홀 문제가 언급되었던 장면입니다.
몬티홀 풀이 : 직관적인 접근
먼저 가장 쉽게 이해하려면 이렇게 생각해 보세요. 처음에 자동차를 고를 확률은? 1/3이죠. 처음에 염소를 선택할 확률은? 당연히 2/3이고 이 둘의 확률총합은 1이 됩니다.
✨ 내가 고른 문에 자동차가 있을 확률 : 1/3
☹️ 내가 고르지 않은 2개의 문 중 하나에 자동차가 있을 확률 : 2/3
자 여기서 중요한 점!! 내가 고른 문에 자동차가 있을 확률 1/3이 몬티홀이 염소 하나를 보여주고 난 후에 바뀔까요? 그렇지 않습니다. 내가 선택하는 시점에는 1/3의 확률인 상태에서 골랐기 때문에 그 다음에 무슨일이 일어나든 내가 고른 문에서 자동차가 나올 확률은 1/3입니다.
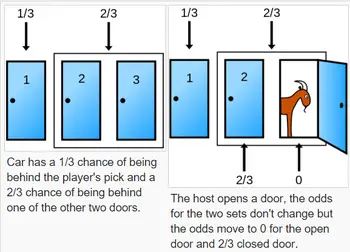
마찬가지로 내가 고르지 않은 두개의 문 중 하나에 자동차가 있을 확률은 2/3입니다. 몬티홀이 염소 하나를 보여주던 안보여주던 선택하지 않은 두개의 문 중에 자동차가 있을 확률은 여전히 2/3입니다. 이게 핵심입니다.
자 그럼 내가 고르지 않은 문에서 자동차가 나올 확률이 2/3인데, 염소를 하나까고 바꿀지 물어본다는 것은 어떤 의미일까요?
이것은 당신이 고르지 않은 ‘2개의 문’을 선택할 기회를 드린다는 뜻이 됩니다. 말그대로 1/3의 당첨확률을 2/3로 바꿔드린다는 것이죠. 무조건 바꾸는게 이익이다. 잘 따라오다가 갑자기 좀 갸웃갸웃 해지셨나요?
알쏭달쏭하다면 문의 개수를 늘려서 생각해보면 더 이해하기가 쉽습니다. 예를 들어 100개의 문으로 이 몬티홀 문제를 낸다고 가정해볼게요.

100개의 문 중에서 하나를 선택했습니다. 진행자가 나머지중 98개의 꽝을 연 뒤 딱 두개만 남겨놓고 바꿀건지 묻습니다. 이 경우에는 당신이 처음에 문을 잘 찍어서 상품을 맞출 확률이 1/100밖에 되지 않죠. 처음의 선택이 거의 항상 틀린다고 생각해도 될 정도입니다. 처음 선택이 틀렸을 가능성이 높으니 당연히 바꾸는게 승산이 있겠죠?
극단적으로 문이 1억개가 있다고 해볼까요? 1억개 중에 여러분이 문 하나를 골랐는데 맞출 수 있을까요? 무조건 틀리겠죠. 자 그러면 당신이 (거의) 100% 확실하게 틀린 문을 골랐습니다. 그리고 진행자가 나머지 문 중에 한개만 남기고 꽝인 문을 모두 열어서 보여주었어요. 그러면 안열고 남겨둔 마지막 남은 문 한개는 뭘까요? 승산이 아니라 이때는 그냥 당첨된거 가져가라는 뜻과도 같습니다.
몬티홀 딜레마는 이렇게 확률의 전가가 핵심입니다. 처음에 문을 하나 고르는 확률에서 나머지 문을 동시에 고르는 확률로 이동할건지 묻는 것입니다. 문이 3개였을 때는 1/3에서 2/3로 바꿀건지 묻는 것이고, 문이 100개였을 때는 1/100인데 99/100로 바꾸실래요? 묻는 것이고 1억개였을 때는 99999999/100000000의 확률로 바꾸라는 것입니다. 꽝을 보여주었기 때문에 가능해지는 일입니다.
문티홀 문제 경우의 수 따져보기
아예 선택 가능한 모든 경우의 수를 따져보고 증명해봐도 됩니다.
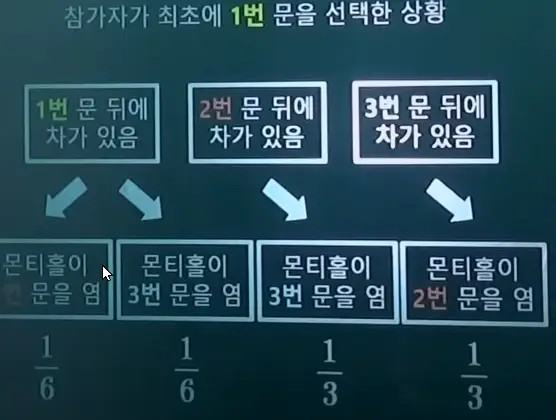
참가자가 1번 문을 선택한다고 합시다. 이 때 상품의 가능한 배치는 (차 염소 염소) (염소 차 염소) (염소 염소 차) 이렇게 3가지입니다. 각각의 사건 발생확률은 1/3씩이 되겠죠.
차가 1번 문에 있었다면 몬티홀은 2번문을 열 수도 있고 3번문을 열 수도 있습니다. 반반의 확률이므로 1/2씩 곱해져서 1/3 * 1/2 = 1/6의 확률이 됩니다. 2번문에 차가 있었다면 몬티홀은 3번 염소를 보여주는 선택지밖에 없으므로 처음의 1/3 확률이 그대로 이어집니다. 3번문에 차가 있을때도 마찬가지로 몬티홀은 2번 염소를 보여주는 선택지밖에 없습니다.
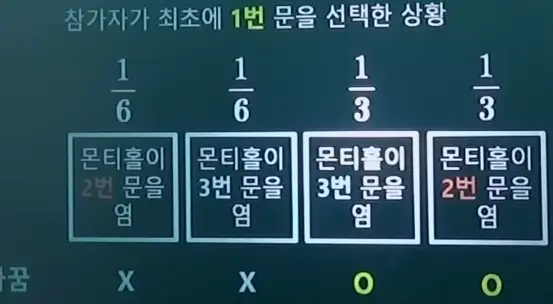
이런 상황에서 선택을 바꾼다면 당첨되는 경우의 수는 (염소 차 염소) (염소 염소 차) 두가지 배치의 경우입니다. 즉 선택을 바꿨을 때 당첨확률 합이 2/3가 됩니다.
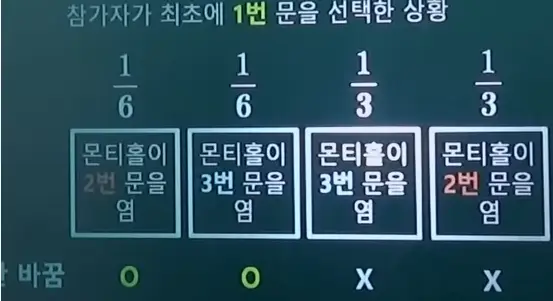
선택을 바꾸지 않는다면 (차 염소 염소)의 경우에 몬티홀이 2번문 또는 3번문을 열어주는 두가지 경우 당첨되므로 1/6 + 1/6 = 1/3이 당첨확률이 됩니다.
이렇게 모든 경우의 수를 나열해봐도 선택을 바꿀경우 2/3 , 선택을 바꾸지 않을 경우 1/3이라는 당첨확률이 나옵니다.
선택을 바꿔도 1/2확률 아니냐에 대한 반론
아무리 해설을 들어도 이해하기가 쉽지는 않은 몬티홀 딜레마 인데요. 가장 헷갈려하시는 부분이 이거에요. 아니 문 하나가 열려서 없어졌으니 남은 2개의 문 중에 하나니까 1/2 아닌가요?
이 말이 성립하려면, 플레이어가 문을 고르기 전에 미리 염소 문을 하나 까서 보여주고 시작해야 합니다. 처음부터 꽝인 문을 하나 보여주고 없애버린 다음, 자 둘 중 하나를 골라보세요 이러면 당첨확률이 1/2입니다.
또는 몬티홀도 어디에 차가 있는지 모르고 무작위로 하나를 뽑았는데 염소가 나왔다고 합시다. 그럼 남은 문 두개 중에 차가 있을 것이고 그 확률은 1/2이 되겠죠.
하지만 몬티홀 문제에서는 진행자가 꽝이 어디있는지 알고 있어서 반드시 꽝 선택지를 제거한다는 전제가 깔려있기 때문에 이러한 반론이 성립하지 않습니다. 몬티홀이 무작위로 문을 열었는데 차가 나와버리면 게임 진행이 망하겠죠. 이러한 경우는 애초에 발생하지 않는 겁니다.
꽝을 제거하고 1/2이 되는것이 아닙니다. 위에서 말했듯 꽝을 포함한 두개의 선택지를 가져갈 수 있게 해준다는 개념으로 보시면 되겠습니다.
문티홀문제 베이즈 정리로 풀기
지금까지의 설명은 직관적으로 그렇구나 하고 이해를 하기 위함이었습니다. 확률통계 관점에서 조건부 확률 베이즈 정리로 수학적인 풀이를 해보겠습니다.
먼저 몬티홀 문제에서 일어날 수 있는 몇 가지 사건들의 확률을 정의합니다.
출연자는 A문을 선택했다고 할 때,
자동차가 A문에 있을 확률 P(차A) = 1/3
자동차가 B문에 있을 확률 P(차B) = 1/3
자동차가 C문에 있을 확률 P(차C) = 1/3
몬티홀이 A문을 열 확률 P(몬A) = 0
몬티홀이 B문을 열 확률 P(몬B) = 1/2
몬티홀이 C문을 열 확률 P(몬C) = 1/2
베이즈 정리 수식
P(A|B) = P(B|A)P(A) / P(B)
여기서 우리가 알고자 하는 확률은 몬티홀이 B문을 열어 염소문을 보여주었을 때, 참가자가 고른 문 A가 당첨일 조건부 확률 P(차A|몬B) 입니다.
베이즈 정리에 의해, P(차A|몬B) = P(몬B|차A)P(차A) / P(몬B)
차가 A에 있으면 몬티홀은 문B C 중에 한개를 열게 되므로 P(몬B|차A) = 1/2
P(차A|몬B) = P(몬B|차A)P(차A) / P(몬B) = (1/2)*(1/3) / (1/2) = 1/3
즉, A를 골랐는데 몬티홀이 B문을 열었을 때 A가 자동차일 확률은 1/3 입니다. 그렇다면, 이 때 몬티홀이 열지않은 문 C가 자동차일 확률은 얼마일까요? A를 골랐는데 차가 C에 있으면 몬티홀은 무조건 B를 열게 되므로 P(몬B|차C) = 1
P(차C|몬B) = P(몬B|차C)P(차C) / P(몬B) = (1)*(1/3) / (1/2) = 2/3
즉, A를 골랐는데 몬티홀이 B문을 열었을 때 C가 자동차일 확률은 2/3 입니다. 그래서 C로 바꿀래? 라고 물었을 때 바꾸는 것이 확률적으로 가능성이 높아지는 결과가 됩니다. 몬티홀이 C문을 열었을 때로 계산한다고 해도 당연히 동일한 수치가 나오죠.
직접 이렇게 풀어보면 단지 베이즈 정리 수식을 외우는게 중요한게 아니라, 상황에 맞게 어떠한 조건부 확률을 정의하고 구해야하는지 개념적으로 접근하는 것이 필요합니다.
참고영상 : 이상엽 수학의신
여러가지 칼럼과 동영상 강의들을 찾아보면서 몬티홀 문제에 대해 가장 설명을 잘한 유튜브 클립을 소개해 드립니다. 수학의 신이라는 유튜브 채널을 운영중인 이상엽 선생님입니다. 추천하는 이유는 목소리도 좋고 목소리도 좋고 목소리도 좋고 ㅋㅋㅋ…
내용도 체계적으로 설명하면서 왜 여러가지 오류와 반론들이 나왔는지에 대해서까지 조목조목 잘 짚어주십니다. 사실 이 동영상 하나만 봐도 몬티홀 문제를 직관적으로 완벽히 이해하는데 전혀 어려움이 없으시리라 생각됩니다.
수학의 대중화를 꿈꾸며 전파하는 분이라는데 나중에 확률 통계 진도 나갈때나 선형대수학 같은거 보다가 막히면 종종 또 찾아봐야겠네요.
참고영상 : 남휘종 숲들숲들
아니 몬티홀 문제풀이를 찾다가 숲들숲들을 보게 될 줄이야 ㅋㅋㅋㅋ
남휘종도 설명을 잘하긴 하는데 뭐랄까 이빨 캐릭터같은 느낌은 지울수가 없네요. 그리고 문 개수 늘려서 설명하는 부분까지는 이해 잘 되게 해주는데, 30개 중에서 하나를 고르고 나머지 중에 꽝을 보여줬을 때 확률이 1/29로 올라간다는 부분은 납득이 안됩니다. 그렇게 설명하면 이 몬티홀 문제 풀이랑 모순되는거 아닌가요.
몬티홀 문제에서도 염소 하나를 보여주는 순간 내 당첨확률이 2/3로 올라간다고 생각해야 될텐데 흠… 합리적인 선택을 한다면 문을 바꾸는게 무조건 유리하니 당첨확률이 2/3으로 올라간다고 보는것도 맞는거 같기도 하고요. 아무튼 보다보면 이해되는 듯 하다가 다시 헷갈려지는 영상입니다.
오늘은 조건부 확률과 베이즈 정리를 공부하다가 잠시 재미를 위해서 몬티홀 딜레마까지 정리해 보았습니다. 헷갈리셨던 부분 말씀히 이해되셨길 바라겠습니다.
